3.2 Entropy and Heat¶
Overview¶
Although we have a mathematical understanding of temperature and entropy now, in practice, that is not always useful. We can only calculate entropies and temperatures of a few ideal cases. However, given our understanding of these ideal cases we are able to extract macroscopic properties of all kinds of matter.
Review¶
Temperature is defined as:

Entropy is defined as:
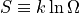
Where 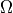 is the multiplicity of the measured state.
is the multiplicity of the measured state.
Predicting Heat Capacity¶
The heat capacity is defined as:
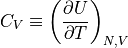
If we can get some formula for the internal energy with respect to the temperature, we can calculate the heat capacity, which really gives us the quantity we are typically interested in. Knowing the temperature is nice, knowing the internal energy is nice, but what really matters is how that energy changes as the temperature changes.
For an Einstein Solid, we know have a formula for U and T and can write the
heat capacity for the case when 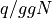 as:
as:
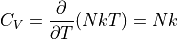
For a monatomic ideal gas:
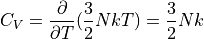
Note that the heat capacity doesn’t change according to the temperature – in the limits these formulas represent. If you start to approach the edge of these limits, then you will find that the heat capacity does indeed change because the assumptions no longer hold.
It is not surprising that the heat capacity is simply  . If it were
something else that would have been surprising.
. If it were
something else that would have been surprising.
The Einstein Solid and Ideal Gas, however, are not representative of everything we might encounter. In section 3.3, we’ll look at paramagnets, which have very surprising behavior in how they share their energy.
How We Got Here¶
Schroeder lists 5 steps that we went through to arrive at these conclusions.
Use QM and combinatorics to calculate
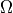 in terms of U, V, N,
and any other relevant variables.
in terms of U, V, N,
and any other relevant variables.Find the entropy with the log of
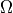 .
.Differentiate S with respect to U to find the temperature as a function of U and other variables.
Rewrite U(T) into T(U).
Differentiate U with respect to T to find an actually useful quantity, the heat capacity.
The challenge is that step 1 is only possible for a few ideal cases.
For the non-ideal cases, we can find step 4 without even knowing how to calculate entropies and multiplicities. We’ll do that in chapter 6.
Given the limitations of what we just did, it’s still useful because it gives us a sort of baseline to compare everything with, and it gives us some degree of insight into systems that aren’t ideal.
Problem 3.8¶
Calculate the heat capacity of the low-temperature Einstein Solid based on the results of problem 3.5.
Measuring Entropies¶
Even in the cases where we have no idea what the formula for the entropy might
look like, we can still calculate the change in entropy, and derive useful
information about the substance. If we start at step 5, and calculate the heat
capacity, we can go to step 4 and calculate how the internal energy depends on
the temperature. With that, we should be able to integrate to find the formula
for the entropy, or at least 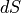 , how the entropy changes, which is
typically all we really need to know about entropy. That is to say, the total
entropy doesn’t matter: Only the fact that entropy increases is relevant, and
so we’d like to know which direction “increasing entropy” is, and make
predictions based solely on that.
, how the entropy changes, which is
typically all we really need to know about entropy. That is to say, the total
entropy doesn’t matter: Only the fact that entropy increases is relevant, and
so we’d like to know which direction “increasing entropy” is, and make
predictions based solely on that.
With constant volume and no work:
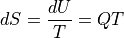
Recalling our discussion about heat capacities, you can trip yourself up if
you’re not carefully keeping things constant. In this case, constant volume
isn’t always an option in many cases. However, in section 3.4 we’ll talk about
quasistatic processes and how we get around this limitation in practice
without spoiling the math. The punchline is that 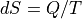 even for
quasistatic cases.
even for
quasistatic cases.
In the cases where internal energy is increasing, but temperature is not changing (IE, melting ice, phase transitions), we can use the formula:
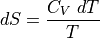
What if we have 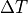 , not an infinitessimally small
, not an infinitessimally small 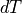 ?
?
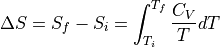
Typically 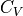 doesn’t change much as the temperature changes, but in
low temperatures it may change quite a bit. So pay attention and you can take
it out of the integral sometimes.
doesn’t change much as the temperature changes, but in
low temperatures it may change quite a bit. So pay attention and you can take
it out of the integral sometimes.
Example¶
If we were to raise 200g of water from 20 degrees C to 100 degrees C, how much did the entropy increase by?
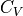 remains constant in this temperature range, which is 200 cal/K
or 840 J/K.
remains constant in this temperature range, which is 200 cal/K
or 840 J/K.
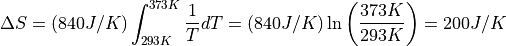
Remember that entropy is a logarithm, so this is a huge increase of
multiplicity – 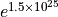 – one of those “beyond
astronomical” numbers.
– one of those “beyond
astronomical” numbers.
Absolute Entropy and S(0)¶
If you know what 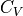 is all the way down to absolute zero, then you
can calculate the total entropy:
is all the way down to absolute zero, then you
can calculate the total entropy:
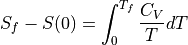
What is the entropy at absolute zero? Multiplicity should be 1 (no energy) and thus entropy is 0. This is the Third Law of Thermodynamics: The entropy at absolute zero is zero.
Although this is theoretically clean, in practice getting a substance down to the minimum energy is all but impossible. Sometimes there are ways to hide tiny amounts of energy in something as simple as orientations of a crystal, so we talk about the residual entropy – and just call that zero since it’s close enough. This is the log of the number of ways to arrange the substance at or near zero energy.
Recall that we found that simply by mixing two things together will result in more entropy than if we had mixed the same things together. Given the fact that even pure atomic substances contain isotopes that are distinguishable, there is no minimum reachable configuration that represents the absolute zero unless you can somehow freeze the atoms in specific positions.
There’s a footnote about Helium, which would remain a liquid at absolute zero, and so would separate its isotopes out by weight and so would reach a minimum state despite it being mixed.
Another form of “residual entropy” is the spin of the nuclei. If we were to reach absolute zero, then the nuclei should all align with each other, but this occurs at such ridiculously low temperatures that we can’t really measure it, and so we chalk it up to residual entropy.
There is a lot of experimental data that we have accumulated where we have calculated the absolute entropy of certain substances. Oftentimes, these experimental results do not concern themselves with residual entropy or mixing of isotopes and such, but they are somewhat useful regardless.
Looking at the integral, it looks like the entropy near zero T would blow up.
However, if we allow 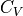 to tend towards 0 as T approaches 0, we can
do some calculus sleight of hand to alleviate such worries.
to tend towards 0 as T approaches 0, we can
do some calculus sleight of hand to alleviate such worries.
This rule, that the heat capacity approaches 0 as the temperature approaches 0 is sometimes called the Third Law of Thermodynamics.
If you did problem 3.8 you would have seen that all the degress of freedom disappear as the temperature approaches 0. That is, the heat capacity disappears. We’ll see this pattern appear multiple times.
If you’re wondering why the heat capacities of ideal gases and high-temperature einstein solids don’t lose their heat capacity as temperature falls near 0, well, that’s simply because of the assumptions we made contradict this.
Problem 3.9¶
Calculate the residual entropy of CO. In other words, if you have N CO atoms, and they can either align as OC or CO, with no effect on energy, how many combinations are there with zero energy?
The Macroscopic View of Entropy¶
The way I was taught thermodynamics was from the macroscopic view. We were told to hold all questions about what entropy is, its connection to statistical mechanics, and the true nature of temperature until after we had walked through all of the macroscopic behaviors of the real world.
This isn’t a bad way to learn thermal physics – it’s probably what I would recommend today. The macroscopic stuff is actually useful, while the statistical mechanics part only seems to explain why and then uncover some really exotic things we might not have been able to find otherwise.
Well, if you skipped chapter 2, you should be fine with the following discussion. If you didn’t skip chapter 2, then you should at least temporarily forget what you learned, so we can look at entropy purely as a macroscopic quantity, similar to T, V, N, or whatever.
The macroscopic definition of entropy is simply:
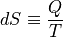
That explains why entropy has units of J/K.
When we first discovered this useful quantity, we didn’t have any idea where it came from or why it existed. It seemed fundamental.
Suppose we have two massive objects, A and B. Both are very, very large, and so will take a very long time to change their temperatures. The first object A is at 500K, and the other object, B, is at 300K.
Say that we let them into thermal contact, and 1500 J flows from A to B. Since object A is hotter, the change in entropy is smaller. And since B is cooler, it has a larger increase in entropy.
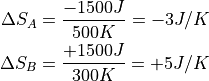
The weird thing is that entropy is not quite like energy. It isn’t conserved – it is always created. Object B has accepted 5 while A has lost 3. And because heat always flows hot to cold, there is nothing anyone can do about this as long as energy is conserved!
Schroeder shares an admittedly flawed model of how entropy works. When energy leaves a system, it takes a little bit of entropy with it. Then, somewhere in between the two systems, its entropy increases, and it takes that new created entropy, along with the lost entropy, into the system. Entropy is kind of like energy, but it has the property of doubling or whatever whenever it crosses systems.
I like to think about it as some sort of currency exchange. The energy in A is worth such-and-such entropy. When you take that energy out of A and convert it to the universal standard currency – whatever that is, maybe gold or silver or some other precious metal – and then take it to B, you have to convert it into the currency that B uses, which has a higher rate of exchange of energy for entropy. You still get the goods – the energy – but you had to pay a price for it. In other words, there is something about A and B that makes energy worth more or less entropy, and it has to do with their temperature. Temperature, therefore, is connected to entropy, as a sign that says, “Your entropy is worth MORE here” if the temperature is less.
This gets back to the “silly analogy” we had of the people trying to maximize happiness. The money they are sharing with each other is energy, and their happiness is entropy. The money is worth different amounts of entropy depending on where it ends up, and so the money will flow until moving money won’t increase entropy anymore. Temperature is a sign of how much a system is willing to share energy because it simply isn’t creating much entropy with it, and cooler systems will do a better job.
Problem 3.10¶
Calculating entropy of melting ice and kitchens.
Problem 3.11¶
Entropy of mixing warm and cold water. Thanfully, the heat capacity of water is (mostly) constant in these temperature ranges, so you just have to find (a) what the resulting temperature is and (b) how much entropy was gained / lost to get there.
Problem 3.12¶
You need two temperatures: Your house and a cold winter day. If you live in a warm climate where the idea of closing windows to trap heat inside your house sounds absurd, use room temperature for your house and 0 celsius for the world.
Then you need to figure out how much energy is lost. This depends on how well-insulated your house is and how big it is. You can go look up your heating bill and calculate how much energy you used to heat the house (and if you’re trying to create heat, then you’re going to be able to perfectly transform energy into heat! It’s when we want to do work with energy that we have to worry about efficiency.) Unfortunately I don’t have a good number for this, so just pick something that sounds reasonable if you don’t want to estimate it.
Problem 3.13¶
For (a), you simply need to know how much energy is transferred from the sun to the earth. Assume that the energy is perfectly absorbed, or don’t, it’s up to you. (If you know what albedo is in relation to planets, then you can look up earth’s albedo.) You may also want to consider that the sun can only ever shine on HALF the earth at a time, or rather, just use the cross-sectional area of the earth if you don’t want to integrate over dot products of the area vectors and sunlight direction.
For (b), I want you to consider several things: (a) what is the entropy of grass versus not-grass? (b) why using “disorder” is a bad, bad thing in certain cases like this.
Problem 3.14¶
At certain temperature ranges, alpha will dominate, and at others, beta will dominate, but at some point, you’ll approach the high-temperature Einstein Solid limit where the heat capacity is constant.
You may also want to draw a quick graph of this. Just superimpose the alpha and beta terms on each other. Or use a spreadsheet to see how it works.
Note that at T=0, the heat capacity is zero, which is what we want to see to maintain our sanity.
Problem 3.15¶
Heat capacity of a star is enough information to calculate the total entropy of the star. No spoilers for you, unfortunately.
Problem 3.16¶
You’re going to have to assume that there is a certain amount of energy that is different for ones and zeros, and that energy only depends on the 1 and the 0, not the position of the 1s and 0s. This is not unlike what we did in chapter 2 where we said “q energy packets” rather than talking about the internal energy. Obviously, you’ll need a factor to relate q to U.
Patreon¶
Thank you to Tony Ly for supporting my channel at the $20 level on Patreon.
While I greatly appreciate supporting my channel through Patreon and the Amazon affiliate links in the description, if you can’t do this then please consider simply sharing my channel with your friends. I think in the long run this will have the most significant benefit for all of us.

